Scripts

Check out my pages on Github: https://github.com/christianepeters

Selected repositories:

  • homomorphic-encryption – how to install helib, SEAL, fhe-toolkit-linux, etc
  • howto – collection of scripts and configuration guidelines (from Docker to Belgian eiD card)
  • coronalert – Python script to validate test codes for the Belgian privacy-friendly Corona alert app
  • phdthesis
  • bibtex
  • wild – decoder for alternant codes (“wild Goppa codes”)
  • isdf2 – information-set decoding for binary codes
  • isdfq – information-set decoding for q-ary codes
  • 2reg – information-set decoding for code-based hash functions

Archive:

Here you find some old material related to research I did a couple of years ago. The content is no longer maintained.

  1. Iteration and operation count for information-set decoding over Fq
  2. Wild-Goppa-code decoder
  3. Complexity approximation 2-regular syndrome decoding

1. Iteration and operation count for information-set decoding over Fq

My paper Information-set decoding for linear codes over Fq presents a new algorithm for decoding linear codes over arbitrary finite fields Fq.

Crude approximation (Pari script)

If the field size q is large then the cost of the first step (updating the matrix) becomes negligible since the cost of the algorithm is dominated by the search for 2p columns adding up to 0 on l positions. One can afford to choose k columns uniformly at random at the beginning of each iteration and then perform a full Gaussian elimination with respect to those k columns.
In order to get a good estimate for the running time you can use the PARI/GP script isdfq.gp to estimate the cost of information-set decoding (ISD). If you care only about q=2 have a look at isdf2.gp.

Note that this rather crude approximation gives a running time which is worse by a factor of 2 or more than the Markov-chain analysis below. It’s fine if you just want to know in which ballpark your parameters are.

If q is small (q=2, q=3, maybe some cases where q=4) it makes sense to speed up the first step (definitely for q=2, see our PQCrypto’08 paper).

Markov-chain computation (using MPFI lib)

The ISD algorithm is probabilistic in that it makes random choices. To compute the average number of iterations it is necessary to analyze a Markov chain. For each choice of parameters of the decoding algorithm the following C program computes the expected number of iterations as well as the number of bit operations needed.

If this approach is used to estimate the security of a code-based cryptosystem against information-set-decoding attacks, the user must run the program repeatedly to search a range of parameter choices for the decoding algorithm. For example, trying this program with a wide range of algorithm parameters for decoding 48 errors in a [961,771] code over F31 identifies the parameters p=2, l=7, c=12, and r=1 as optimal and shows that 2128 bit operations are used by the information-set-decoding attack, as reported in the paper.

In fact, it was used to search a range of attack parameters against a range of codes over F31 to identify this code with [961,771,>=96] as having minimal keysize k x (n-k) among all codes over F31 that require at least 2128 steps in the decoding algorithm.

See below for an explanation of how to use the isdfq.c program and several examples.

Download from my GitHub repos: isdfq.c

  • The isdfq.c program uses the MPFI library which is built on top of the MPFR library, which is built on top of the GMP library.
  • This program works for any field Fq, including the binary case.
    This program supersedes the program given for binary codes whose record can be found in the repository
    https://github.com/christianepeters/isdf2/.
  • The isdfq.c program takes the following 13 inputs:
    • field size q (default 31)
    • code length n (default 961);
    • code dimension k (default 771);
    • number of errors w (default 48);
    • algorithm parameter p (default 2);
    • algorithm parameter l (default 20);
    • algorithm parameter m (default 1);   (*)
    • algorithm parameter c (default 7);
    • algorithm parameter r (default 1);
    • use overlapping sets by setting fs=1; (default 0);
    • algorithm parameter M for the fs=1 case (adjust number of subsets by multiplying the standard choice binomial(k,p)/sqrt(binomial(2p,p)) by a factor of M) (default 1.);
    • look for a weight-w word by setting mww=1; (default 0);
    • adjust precision by setting prec (default 300).
  • The user can confirm a choice of parameters for the algorithm using this program. The program does not choose the best algorithm parameters itself. The user should loop over all suitable choices for p,l,m,c,r, and M in order to figure out the lowest cost for an attack.
  • Examples:
    • Compile using gcc -o isdfq isdfq.c -lm -lgmp -lmpfr -lmpfi
    • Run ./isdfq to get the number of operations for decoding 48 errors in a [961,771] code over F31 with parameters p=2, l=7, c=12, r=1.
      q=31 n=961 k=771 w=48 p=2 l=7 m=1 c=12 r=1:
      bit ops 129.023892, bit ops per it 32.208747,
      log2 #it 96.815146
    • Run ./isdfq 4 2560 1536 128 2 15 1 8 4 0 1 0 400
      to get the number of operations it takes to find a weight-128 word in a [2560,1536] code over F4 when using parameters p=2, l=15, m=1, c=8, and r=4.
      q=4 n=2560 k=1536 w=128 p=2 l=15 m=1 c=8 r=4:
      bit ops 181.857556, bit ops per it 27.515332,
      log2 #it 154.342224
    • Run ./isdfq 2 1024 524 50 2 20 2 7 7 to get the numbers of operations to decode 50 errors in a [1024,524] binary code using parameters p=2, l=20, m=2, c=7, r=7.
      q=2 n=1024 k=524 w=50 p=2 l=20 m=2 c=7 r=7:
      bit ops 60.179978, bit ops per it 21.864968,
      log2 #it 38.315010
    • Run ./isdfq 2 1024 525 50 2 20 2 7 7 0 1. 1 to get the number of operations it takes to find a weight-50 word in a [1024,525] binary code using the algorithm with parameters p=2, l=20, m=2, c=7, r=7 (note that the value of mww is set to 1).
      q=2 n=1024 k=525 w=50 p=2 l=20 m=2 c=7 r=7:
      bit ops 60.392514, bit ops per it 21.944141,
      log2 #it 38.448373
  • Cost of attacking codes proposed by

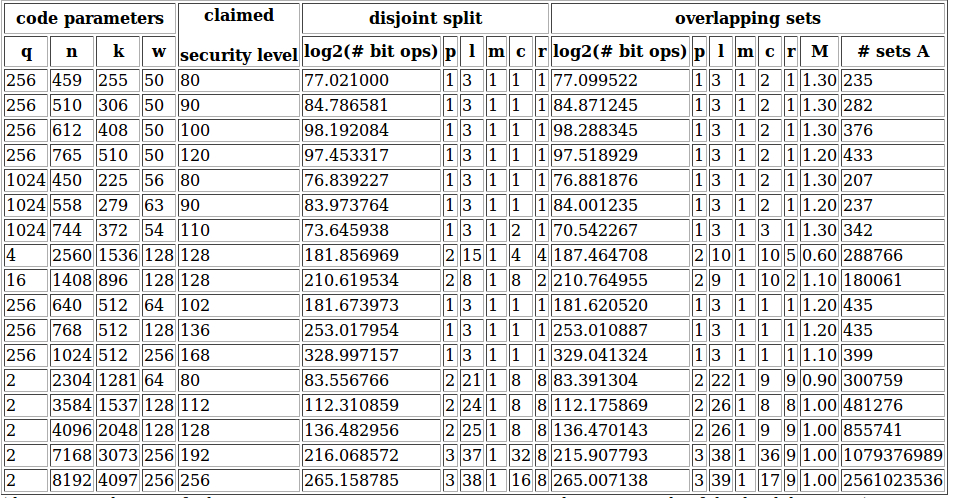
    isdfq table; Table 6.1 on page 119 in my Ph.D. thesis

    The commands to verify these parameters are:

    ./isdfq 256 459 255 50 1 3 1 1 1 0 1.00 0 300
    ./isdfq 256 459 255 50 1 3 1 2 1 1 1.30 0 300
    ./isdfq 256 510 306 50 1 3 1 1 1 0 1.00 0 300
    ./isdfq 256 510 306 50 1 3 1 2 1 1 1.30 0 300
    ./isdfq 256 612 408 50 1 3 1 1 1 0 1.00 0 300
    ./isdfq 256 612 408 50 1 3 1 2 1 1 1.30 0 300
    ./isdfq 256 765 510 50 1 3 1 1 1 0 1.00 0 300
    ./isdfq 256 765 510 50 1 3 1 2 1 1 1.20 0 300
    ./isdfq 1024 450 225 56 1 3 1 1 1 0 1.00 0 300
    ./isdfq 1024 450 225 56 1 3 1 2 1 1 1.30 0 300
    ./isdfq 1024 558 279 63 1 3 1 1 1 0 1.00 0 300
    ./isdfq 1024 558 279 63 1 3 1 2 1 1 1.20 0 300
    ./isdfq 1024 744 372 54 1 3 1 2 1 0 1.00 0 300
    ./isdfq 1024 744 372 51 1 3 1 3 1 1 1.30 0 300
    ./isdfq 4 2560 1536 128 2 15 1 4 4 0 1.00 0 400
    ./isdfq 4 2560 1536 128 2 10 1 10 5 1 0.60 0 400
    ./isdfq 16 1408 896 128 2 8 1 8 2 0 1.00 0 400
    ./isdfq 16 1408 896 128 2 9 1 10 2 1 1.10 0 400
    ./isdfq 256 640 512 64 1 3 1 1 1 0 1.00 0 300
    ./isdfq 256 640 512 64 1 3 1 1 1 1 1.20 0 300
    ./isdfq 256 768 512 128 1 3 1 1 1 0 1.00 0 500
    ./isdfq 256 768 512 128 1 3 1 1 1 1 1.20 0 500
    ./isdfq 256 1024 512 256 1 3 1 1 1 0 1.00 0 750
    ./isdfq 256 1024 512 256 1 3 1 1 1 1 1.10 0 750
    ./isdfq 2 2304 1281 64 2 21 1 8 8 0 1.00 0 300
    ./isdfq 2 2304 1280 64 2 22 1 9 9 1 0.90 0 300
    ./isdfq 2 3584 1537 128 2 24 1 8 8 0 1.00 0 300
    ./isdfq 2 3584 1536 128 2 26 1 8 8 1 1.00 0 350
    ./isdfq 2 4096 2048 128 2 25 1 8 8 0 1.00 0 400
    ./isdfq 2 4096 2048 128 2 26 1 9 9 1 1.00 0 400
    ./isdfq 2 7168 3073 256 3 37 1 32 8 0 1.00 0 600
    ./isdfq 2 7168 3072 256 3 38 1 36 9 1 1.00 0 700
    ./isdfq 2 8192 4097 256 3 38 1 16 8 0 1.00 0 700
    ./isdfq 2 8192 4096 256 3 39 1 17 9 1 1.00 0 700

(*) The algorithm looks for words having weight p among the positions indexed by a set X, weight p among the positions indexed by a set Y and weight 0 among l positions indexed by a set Z.
In the paper Attacking and defending the McEliece cryptosystem Dan Bernstein, Tanja Lange, and I proposed to speed up Stern’s algorithm for codes over F2 by taking m sets Z1,…,Zm outside the information set, each with l positions and to look for words having weight p among the X-indexed positions, weight p among the Y-indexed positions, and weight 0 among the positions indexed by one of those sets Zj. For small q, such as q=2, it turns out that using m>1 provides better results.
For codes over arbitrary fields Fq I considered only one set Z. That’s why the default setting of isdfq.c is m=1.

2. Wild-Goppa-code decoder

Here we make a simple Python script available which demonstrates how to decode wild Goppa codes.
The algorithm is described in detail in the article Wild McEliece by Daniel J. Bernstein, Tanja Lange, and myself.

Download wild-decoder.py

3. Complexity approximation 2-regular syndrome decoding

The paper Faster 2-regular information-set decoding presents an algorithm to speed up information-set decoding attacks on fast-syndrome based hash functions.

Here’s a script in pari that approximates the computations in the paper. The count is not entirely accurate (writing it on request by a student in May 2018) but it gives you the right ball park:

Download 2reg.gp